25학년도 수능

지난주에 치뤄졌던 수능문제를 다뤄볼까 합니다.

시작하기에 앞서, 수험생 여러분들 수능 치르느라 정말 수고 많으셨습니다!!

늘 그래왔듯이 동일한 방식으로 이번 수능 기하 파트를 진행하도록 하겠습니다.

저희는 이번 9월 모의평가 28번을 보았기 때문에 동일한 아이디어를 공유하고 있다는 것을 쉽게 접근할 수 있습니다.

https://jamcoder.tistory.com/entry/25%ED%95%99%EB%85%84%EB%8F%84-9%EC%9B%94-%EB%AA%A8%EC%9D%98%ED%8F%89%EA%B0%80

25학년도 9월 모의평가

 

우선, 항상 말하였지만 곡선 개형이 필요한 것이 아니면 원 O, 즉 원판자취를 미리 그려놓는 행위는 상당한 시간낭비이자 시험지만 지저분해집니다.

9월평가원 28번과 동일한 방식으로 문제풀이를 진행해 보면, 우선 평면 ABC와 원 O의 교선이 선분AB임을 알 수 있습니다.

원 O위의 임의의 점을 X라 하면 이를 정리하여 점 A, B, C, X의 위치관계를 표현하면 아래와 같습니다.

평면 ABC와 원 O는 수직 관계이므로 직선BC가 원 O를 포함하는 평면의 법선임을 알 수 있습니다.

이런 점에서 각(CBX)는 수직임을 알 수 있습니다.

또한, 점X의 경우 원 O위의 점이기도 하지만 구 위의 점이기도 하며 선분AC가 구의 지름이므로 각(CXA) 역시 직각임을 알 수 있습니다.

삼수선의 정리에 따라 각(BXA) 역시 직각임을 알 수 있기 때문에 선분 AB는 원 O의 지름임을 알 수 있습니다.

주어진 조건에 따르면, 점 P, Q에서 선분AC사이의 거리가 4라고 하였는데 이는 원 O의 반지름의 길이와 동일하므로, 점 P와 점 Q는 원 O위의 점이며 지름인 선분AB에서 점 A와 가까운 곳에 위치함을 알 수 있습니다.

원 O의 중심을 점 O'이라 하고, 점 P에서 선분AB에 내린 수선의 발을 점 H라 하면, 이를 정리하면 평면 ABC와 점 P, 점 H의 위치관계는 아래와 같습니다.

(점 Q의 경우 선분 AB를 기준으로 점 P의 대척점에 있다고 보면 됩니다.)

선분PH의 길이를 l이라 하고, 점 H에서 선분AC에 내린 수선의 발을 H'이라 하면,

삼각형 PO'H와 삼각형 PH'H는 RHS 합동임을 알 수 있습니다.

이를 통해 |선분HH'| = |선분HO'| = sqrt(16-l^2)임을 알 수 있습니다.

점 Q는 선분 AB를 기준으로 점 P의 대척점이므로, 선분 PQ의 길이는 2l임을 알 수 있습니다.

삼각형 ACB와 삼각형 AHH'은 AA닮음이므로 아래와 같은 비율이 성립합니다.

|선분AH| : |선분HH'| = |선분AC| : |선분CB| = 4 - sqrt(16-l^2) : sqrt(16 - l^2) = 5 : 3

이를 정리하면 sqrt(16 - l^2) = 3/2이고, 64 - (2l)^2 = 9 임을 알 수 있습니다.

이를 정리하면 2l = sqrt(55)가 나오게 됩니다.

이번 6월과 9월 평가원을 잘 익혀두고 센스만 있다면 상당히 간단히 풀 수 있다고 생각됩니다.

우선, 선분 BC의 중점을 점 M이라 하면, 첫번째 조건을 정리하면 아래와 같습니다.

|XB + XC| = 2|XM| = |XB - XC| = |CB| = 4

이번 9월 모의평가 30번에서 사용한 평행사변형법의 확장에 불과합니다.

https://jamcoder.tistory.com/entry/25%ED%95%99%EB%85%84%EB%8F%84-9%EC%9B%94-%EB%AA%A8%EC%9D%98%ED%8F%89%EA%B0%80

25학년도 9월 모의평가

이를 정리하면 |XM| = 2이며 점 X는 선분BC를 지름으로 하는 원의 일부임을 알 수 있고 점 X의 자취는 아래와 같습니다.

물론, 이는 보여드리기 위해 표현한 것이고 실제로 문제를 풀이할 때는 곡선 개형이 필요하지 않은 이상 시험지에 그리는 것은 상당한 시간 낭비라고 봅니다.

 

두번째 조건을 정리하면 아래와 같습니다.

4PQ = 4PM + 4MQ = PB + 2PD = PM + MB + 2PM + 2MD

이 또한 역시 이번 6월모의평가에서 사용한 다루기 쉬운 정점을 기준으로 식을 통일한 것입니다.

https://jamcoder.tistory.com/entry/25%ED%95%99%EB%85%84%EB%8F%84-6%EC%9B%94-%EB%AA%A8%EC%9D%98%ED%8F%89%EA%B0%80

25학년도 6월 모의평가

이를 정리하면 4MQ = MB + 2MD + MP임을 알 수 있습니다.

 

구하고자 하는 것을 정리하면 아래와 같습니다.

(AC)*(AQ) = (AC)*(AM + MQ) = (AC)*(AM) + (AC)*(1/4)(MB + 2MD + MP)

= (AC)*(AM) + (1/4)(AC)*(MB) + (1/2)(AC)*(MD) + (1/4)(AC)*(MP)

(AC)*(AM), (AC)*(MB), (AC)*(MD)는 상수이므로 (AC)*(MP)의 값에 따라 최대/최소가 결정되는데,

MP는 점M을 중심으로 하는 원 위의 임의의 반지름이므로 AC와 MP가 나란할 때가 최대, 반대일 때가 최소임을 알 수 있습니다.

 

(AC)*(AM), (AC)*(MB), (AC)*(MD)의 경우 계산할때 내적계산을 따로 복잡하게 하지 마시고 아래와 같이 계산하면 많이 수월해집니다.

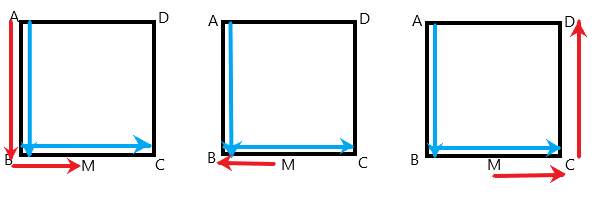
이를 이용하여 정리하면 아래와 같습니다.

(AC)*(AQ) = (AC)*(AM) + (1/4)(AC)*(MB) + (1/2)(AC)*(MD) + (1/4)(AC)*(MP)

= (16 + 8) + (1/4)(-8) + (1/2)((-16) + 8) + (1/4)(AC)*(MP)

= 18 + (1/4)(AC)*(MP)

 

이를 통해 M = 18 + (1/4)|AC|*|MP| = 18 + sqrt(8), m = 18 - (1/4)|AC|*|MP| = 18 - sqrt(8) 이므로,

M*m = 324 - 8 = 316임을 알 수 있습니다.

 

이번, 수능 선택과목 기하의 경우, 올해 6월과 9월의 유형을 대놓고 반영하였다고 보아도 과언이 아닐 정도로 기출만 제대로 살펴보았어도 아무 문제 없이 무난하게 해결하였을 것으로 보이며 수험생들 모두 올해 6월과 9월을 보았기 때문에 체감 난이도는 솔직히 그렇게 크지 않았을 것으로 보입니다.

 

끝으로, 다시 한번 이번 수능 치루느라 고생 많으셨고 모두들 좋은 결과 있기를 응원하겠습니다.

이상입니다.